圆锥曲线学习笔记
圆锥曲线
所有圆锥曲线的大题，先整理再代入，不要着急将直线与圆锥曲线联立。
基础
椭圆的通径：过焦点与 轴平行的线段，
椭圆焦点三角形面积公式：
双曲线焦点三角形面积公式：
抛物线焦点弦
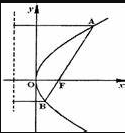
抛物线过焦点的弦的结论： ，其中 于倒斜式 设倒斜式，联立易证。这个在做小题时非常常用。
抛物线弦长公式： 通过焦半径公式可以简单证明。
焦半径公式：，其中 为焦半径与 轴正方向的夹角。
焦半径倒数和为定值：
以某条焦半径(AF 或 BF) 为直径的圆与 y 轴相切。
证明：设中点 ，由第一定义有 ，显然证毕。
以 为直径的圆与抛物线准线相切。 设 垂直准线于 ， 垂直准线于 ，则 A O D 三点共线。
第二定义
圆锥曲线第二定义：点到焦点距离与到准线距离比为离心率。
其中 为到准线距离，准线为 或
焦半径公式
抛物线坐标表示焦半径：
椭圆坐标表示焦半径：
双曲线坐标表示焦半径：
圆锥曲线焦半径角度表示：，其中 为焦准距，即
圆锥曲线极坐标方程：
第三定义
椭圆第三定义
圆锥曲线第三定义：任意中心弦两端点到曲线上一点的斜率乘积为定值。
椭圆：
证明：过原点作中位线，设出中点坐标，点差法表示斜率。
双曲线第三定义
双曲线：
双曲线第三定义证明： 取 ，则 ，且有 对于双曲线上任意一点 有 ，，则 考虑统一消去 ，由椭圆方程有 ，则
中线长公式：
证明：互补角余弦值相加为零
其他结论
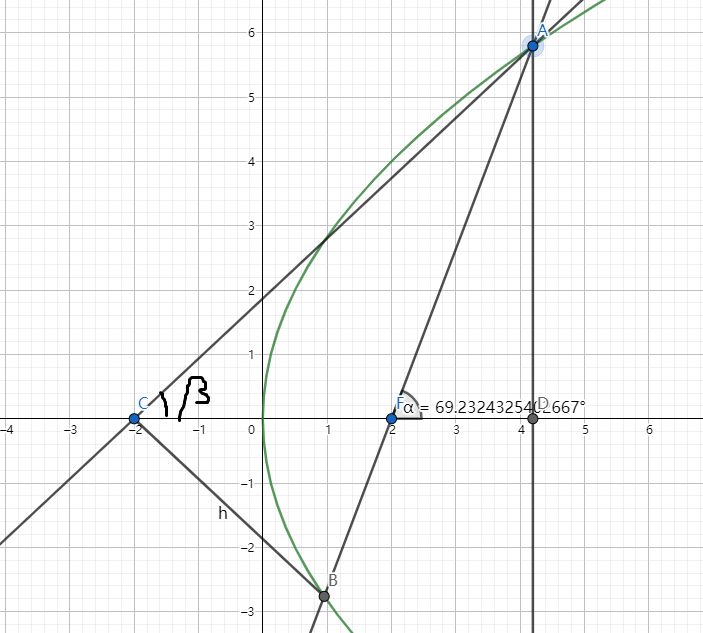
且
小结论：圆锥曲线的切线交两长轴顶点关于 轴的垂线于点 ，则 在以 为直径的圆上。 证明：
背诵内容
椭圆焦半径公式： 在椭圆上， 为离心率，表示 与
抛物线焦半径公式：已知焦点弦与 轴夹角为 ，表示 与 ， 为上方的点。 ， 为下方的点。 实质上， 为与 轴夹角， 自带正负性即可无需分类。
双曲线焦点三角形面积公式？
抛物线中，
抛物线中，焦点弦两点 ，，
抛物线中，焦点弦两点 ，，
抛物线中，焦点弦两点 ，， ，有
抛物线中，焦点弦两点 ，， ，其中 于倒斜式
椭圆通径是什么？长度？ 过焦点与 轴平行的线段。 通径长：
椭圆焦点三角形面积公式？
抛物线焦点弦长公式？
判断：抛物线中以某条焦半径( 或 为直径的圆与 轴相切。 正确。 证明：设中点 ，由第一定义有 ，显然证毕。
判断：抛物线中以焦点弦 为直径的圆与抛物线准线相切。 正确。
抛物线中，焦点弦两点 作准线的垂线，垂直于 两点，则 是多少？AOD 三点的关系？ 共线。
上图中， 表示？ 与 关系？
抛物线中，焦点弦两交点与 的连线的斜率的性质？
圆锥曲线第二定义？ 点到焦点距离，与点到准线距离比为离心率。
圆锥曲线准线？
椭圆焦半径公式， 表示？
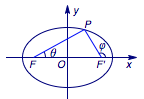椭圆焦半径公式， 表示？
其中 为焦准距，即
圆锥曲线焦准距？
双曲线焦半径公式， 表示？
圆锥曲线统一极坐标方程？
圆锥曲线第三定义？ 任意中心弦两端点到曲线上一点的斜率乘积为定值。
椭圆第三定义？ ，可以通过伸缩变换简单证明。
双曲线第三定义？
中线长公式？ 证明：互补角余弦值相加为零。
判断：圆锥曲线的切线交两长轴顶点关于 轴的垂线于点 ，则 在以 为直径的圆上。 正确。
背诵内容（同步）
抛物线焦点三角形面积公式角度表示？以 与 表示
椭圆焦半径公式，用 表示，需要讨论左右焦点。左右焦点
椭圆焦点弦长公式？